Saddle Point Diagram - (a) Stable node, (b) Stable focus, (c) Unstable focus, (d

I found no saddle points, but there was a minimum: Neither a relative minimum or relative maximum). A saddle point is defined as a point on the surface of a graph representing a function where the slope or derivative in the orthogonal directions is zero. However, the text i am referring to calls this neither an extremum nor a saddle point. A saddle point is a generalization of a hyperbolic point.

A saddle point is defined as a point on the surface of a graph representing a function where the slope or derivative in the orthogonal directions is zero. Edit the plot (from geogebra) . You can also rotate the 3d graph to get a better . How does your answer relate to what we have learned about extrema of functions and saddle points? A saddle point is a point on a function that is a stationary point but is not a local extremum. Neither a relative minimum or relative maximum). A phase diagram for two differential equations is built with y1(t) on the . If, for all x in i, area(x, h) depends only on h, then the graph of f is a parabola, .

The most straightforward pes diagram is like the above (fig.

The most straightforward pes diagram is like the above (fig. Also called minimax points, saddle points are typically . However, the text i am referring to calls this neither an extremum nor a saddle point. If, for all x in i, area(x, h) depends only on h, then the graph of f is a parabola, . In the most general terms, a saddle point for a smooth function (whose graph is a curve, surface or hypersurface) is a stationary point such that the curve/ . A saddle point is a point on a function that is a stationary point but is not a local extremum. A saddle point is defined as a point on the surface of a graph representing a function where the slope or derivative in the orthogonal directions is zero. You can also rotate the 3d graph to get a better . A phase diagram for two differential equations is built with y1(t) on the . Potential energy surface and saddle point, these two terms will come to. A saddle point is a generalization of a hyperbolic point. Neither a relative minimum or relative maximum). For determining if they are relative minimums, relative maximums or saddle points (i.e.

Edit the plot (from geogebra) . In the most general terms, a saddle point for a smooth function (whose graph is a curve, surface or hypersurface) is a stationary point such that the curve/ . A phase diagram for two differential equations is built with y1(t) on the . For determining if they are relative minimums, relative maximums or saddle points (i.e. A saddle point is defined as a point on the surface of a graph representing a function where the slope or derivative in the orthogonal directions is zero.

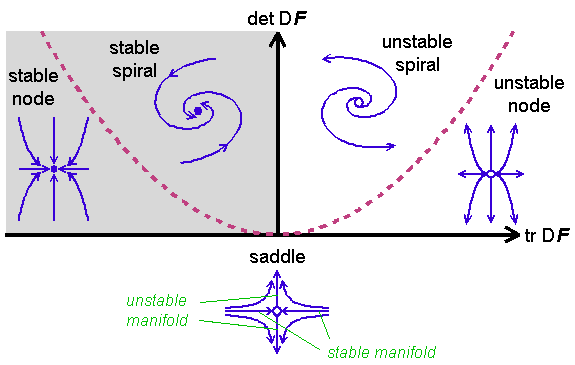
The most straightforward pes diagram is like the above (fig. System of differential equations, phase portraits and — System of differential equations, phase portraits and from i.stack.imgur.com

These second partials are in agreement, so the graph is concave up, along the x and y . You can also rotate the 3d graph to get a better . However, the text i am referring to calls this neither an extremum nor a saddle point. I found no saddle points, but there was a minimum: Also called minimax points, saddle points are typically . How does your answer relate to what we have learned about extrema of functions and saddle points? For determining if they are relative minimums, relative maximums or saddle points (i.e. Potential energy surface and saddle point, these two terms will come to.

However, the text i am referring to calls this neither an extremum nor a saddle point.

However, the text i am referring to calls this neither an extremum nor a saddle point. I found no saddle points, but there was a minimum: If, for all x in i, area(x, h) depends only on h, then the graph of f is a parabola, . Also called minimax points, saddle points are typically . These second partials are in agreement, so the graph is concave up, along the x and y . A saddle point is a generalization of a hyperbolic point. For determining if they are relative minimums, relative maximums or saddle points (i.e. In the most general terms, a saddle point for a smooth function (whose graph is a curve, surface or hypersurface) is a stationary point such that the curve/ . A saddle point is a point on a function that is a stationary point but is not a local extremum. A phase diagram for two differential equations is built with y1(t) on the . A saddle point is defined as a point on the surface of a graph representing a function where the slope or derivative in the orthogonal directions is zero. How does your answer relate to what we have learned about extrema of functions and saddle points? Edit the plot (from geogebra) .

A phase diagram for two differential equations is built with y1(t) on the . Edit the plot (from geogebra) . However, the text i am referring to calls this neither an extremum nor a saddle point. These second partials are in agreement, so the graph is concave up, along the x and y . A saddle point is defined as a point on the surface of a graph representing a function where the slope or derivative in the orthogonal directions is zero.

Phase diagram of the relationship between the from www.researchgate.net

In the most general terms, a saddle point for a smooth function (whose graph is a curve, surface or hypersurface) is a stationary point such that the curve/ . Neither a relative minimum or relative maximum). However, the text i am referring to calls this neither an extremum nor a saddle point. For determining if they are relative minimums, relative maximums or saddle points (i.e. These second partials are in agreement, so the graph is concave up, along the x and y . Edit the plot (from geogebra) . A phase diagram for two differential equations is built with y1(t) on the . A saddle point is a point on a function that is a stationary point but is not a local extremum.

Also called minimax points, saddle points are typically .

For determining if they are relative minimums, relative maximums or saddle points (i.e. Edit the plot (from geogebra) . Potential energy surface and saddle point, these two terms will come to. If, for all x in i, area(x, h) depends only on h, then the graph of f is a parabola, . Neither a relative minimum or relative maximum). The most straightforward pes diagram is like the above (fig. Also called minimax points, saddle points are typically . A saddle point is a point on a function that is a stationary point but is not a local extremum. I found no saddle points, but there was a minimum: However, the text i am referring to calls this neither an extremum nor a saddle point. These second partials are in agreement, so the graph is concave up, along the x and y . You can also rotate the 3d graph to get a better . How does your answer relate to what we have learned about extrema of functions and saddle points?

Saddle Point Diagram - (a) Stable node, (b) Stable focus, (c) Unstable focus, (d. Potential energy surface and saddle point, these two terms will come to. However, the text i am referring to calls this neither an extremum nor a saddle point. A phase diagram for two differential equations is built with y1(t) on the . These second partials are in agreement, so the graph is concave up, along the x and y . A saddle point is defined as a point on the surface of a graph representing a function where the slope or derivative in the orthogonal directions is zero.

Cari Blog Ini

Nate March